Simulated Annealing on TSP

The traveling salesperson problem (TSP) is a well-studied optimization problem which finds the shortest 

path connecting $n$ cities so that each city is visited exactly once. This is a minimization problem where the objective value to be minimized is the total distance travelled.

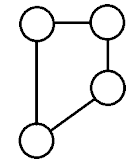A solution of TSP with $4$ cities

Using the formulation of  Dantzig–Fulkerson–Johnson, the problem can be tackled with integer programming. Indeed branch and bound algorithms provide exact solutions to TSP, but since it is an NP-hard problem they can only process small problems containing only 40-60 cities. 

Heuristic approaches provide a faster alternative. The simplest method proposed is the nearest neighbour heuristic which takes the salesperson to the nearest unvisited city at each step of the algorithm. Despite its simplicity the output solution is often sub-optimal, as you can see in figure below.

Black and blue nodes are current and nearest unvisited cities respectively. In the last step, the last visited city is connected to the first city. The route proposed by nearest neighbour is sub-optimal.

TSP can also be considered to be a permutation problem where the solution is a permutation of the set of cities $V=\{1,\dots ,n\}$. A local search algorithm would start at some initial random permutation and iteratively find neighbours of that permutation that improve the objective value. The simplest local search algorithm is the hill climbing method, where a random neighbouring permutation is chosen, provided that it reduces the total distance travelled. Hill climbing terminates when all neighbours of the current solution are worse. A weakness of this method is that it gets trapped in a local optimum and can not get unstuck because all neighbours of the current solution have worse objective 

values.

To alleviate this, simulated annealing proposes that worse neighbouring solution should be accepted with probability $\exp (-\mathrm{\Delta }f/T)$, where $\mathrm{\Delta }f$ is the deterioration in the objective value and $T$ is the "temperature" of the system, which gradually decreases over time/iterations, just like in metallurgical annealing. Initially when the temperature is high, the algorithm explores the solution space by accepting most solutions regardless of how bad they are, but over time 

the algorithm becomes less tolerant of objective value deteriorations. A typical formula of temperature

decay is geometric; the temperature in the $i^{\text{th}}$ iteration is $T_i=T_0{r}^i$. Hill climbing

is a special case of simulated annealing with $T=0$.

Simulated annealing maximizing a function with solution space $\mathbb{R}$. Gif taken from Wikipedia.

Note that we still have not defined what a random neighbouring permutation is. Let $(p_1,\dots ,p_n)$

be the current permutation. To construct the proposed next permutation, two integers $1\le i\le j\le n$ are randomly chosen so that the subpermutation $(p_i,\dots ,p_j)$ is reversed; such an operation is also known as 2-opt. Another operation that is often applied in simulated annealing is the transporting operation where the subpermutation $(p_i,\dots ,p_{j-1})$ is transported after the subpermutation $(p_j,\dots ,p_k)$. A hybrid approach allows the operation to either be transportation or reversal/2-opt with probability $0.5$ for each operation. In the following figures you can see how current solutions (on the left) are transformed under these two operations to the next proposed permutations.

Reverse operation on nodes $4$ and $7$.

Transport operation on subpermutations $(3,4)$ and $(5,6,7)$.

The performance of the Nearest Neighbour heuristic (NN) and Simulated Annealing (SA) is  

summarised in the table that follows. 

	$n=10$	Time(s)	$n=50$	Time(s)	$n=100$	Time(s)	$n=200$	Time(s)
NN	2.06	4e-5	7.04	5e-4	9.11	2e-3	12.88	7e-3
SA	1.9	1.4	5.73	7	8.41	13	11.82	30

SA provides better routes with lower total distance than NN, but takes longer to run and this holds across different problem sizes. 

Check the next blog post on how TSP can be solved using the Genetic Algorithm.